Python Recursion
Here are some questions that a newbie Python user has organized. Most of the topics are examples and exercises from the usual classes and are organized here for review purposes.
Related course: Complete Python Programming Course & Exercises
1. Dichotomies to find the specified value of an ordered array.
Write a program binary_search(x, y), enter a list x (you can assume the data in it is already in ascending order) and enter the data y you want to find, so that the function returns the index of y, or "Not found" when y is not x.
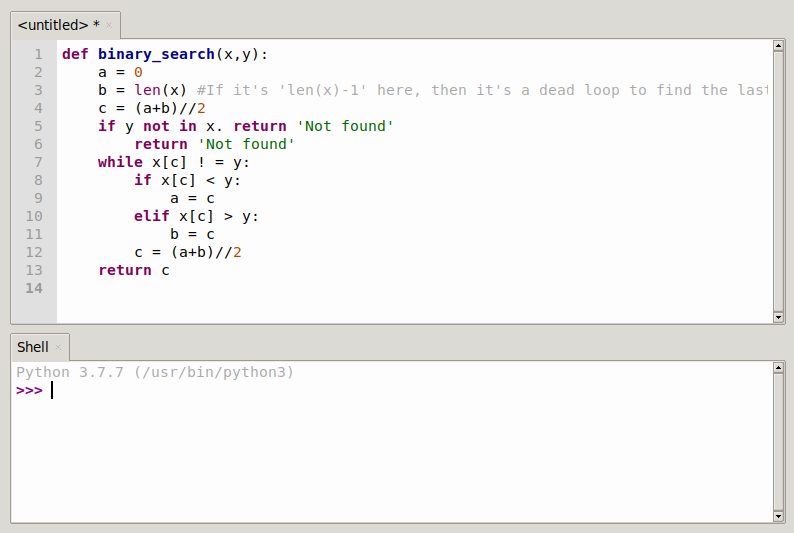
def binary_search(x,y):
a = 0
b = len(x) #If it's 'len(x)-1' here, then it's a dead loop to find the last number
c = (a+b)//2
if y not in x. return 'Not found'
return 'Not found'
while x[c] ! = y:
if x[c] < y:
a = c
elif x[c] > y:
b = c
c = (a+b)//2
return c
This question can only be written as a function of LOOP if it is asked in terms of the question, but it can also be solved by recursion.
def binary_search(min, max, d, n): '''initial mid=0, max=len(d)'''
mid = (min+max)//2
if n not in d. return 'Not found'
return 'Not found'
elif d[mid] < n:
return binary_search(mid, max, d, n)
elif d[mid] > n:
return binary_search(min, mid, d, n)
else:
return mid
2. String (non-duplicate) full alignment
def permutation(array):
if len(array) <= 1:
return [array]
res = []
for i in range(len(array)):
s = array[:i] + array[i+1:] # Take out one element at a time
p = permutation(s) # Arrange the remaining elements in full
for x in p:
res.append(array[i:i+1]+x) #insert this element behind the remaining element
(Or it's as simple as writing a function to get rid of the duplicates.)
3. The stair climbing problem.
(####### 1) Assuming there are n steps, one or three steps at a time, how many possibilities are there to complete this section of steps?
(can be seen as a Fibonacci series)
def func(n):
if n <= 2:
return 1
elif n == 3:
return 2
elif n > 3:
return func(n-1) + func(n-3)
(###### 2) Assuming there are n steps, 1 or 3 steps at a time, list all the possible steps to complete this section
def func(n):
res = []
if n == 1:
return '1'
elif n == 2:
return '11'
elif n == 3:
return ['111', '3']
elif n > 3:
for i in func(n-1):
res.append(i + '1')
for i in func(n-3):
res.append(i + '3')
return res
4. Tower of Hanoi
(####### 1) Suppose there are n discs in total, how many times do you need to move them?
def han(n):
k = 0
if n == 1:
k += 1
elif n > 1:
k += 2*han(n-1) + 1
return k
(##### 2) Assuming there are n discs in total, find the steps for each movement
def han(disc, frm, to, temp):
if disc == 1:
print('move disc' , 1, 'from', frm, 'to', to)
elif disc > 1:
han(disc-1, frm, temp, to)
print('move disc' , disc, 'from', frm, 'to', to)
han(disc-1, temp, to, frm)
5. List each letter in a string in full case
Write a program to read a string input and then output a list of all possible case permutations of the string.
def case_permutation(array):
res = []
if len(array) <= 1:
res.append(array.lower())
res.append(array.upper())
return res
else:
s = array[0]
array = array[1:]
p = case_permutation(array)
for x in p:
res.append(s.lower()+x)
res.append(s.upper()+x)
return res
6. Judgment return.
def is_pal(line):
n = len(line)
if n <= 1:
return True
elif n <= 3:
if linr[0] == line[n-1]:
return True
return False
return False
elif n > 3:
if line[0] == line[n-1]:
return is_pal(line[1:n-1]) '''Delete the first and last characters ''''
return False
return False
7. Looking for a power set.
(Here I've automatically defaulted the set to a list)
def power(s):
res = []
if len(s) == 1:
res.append([s[0]])
res.append([])
elif len(s) > 1:
for i in power(s[1:]):
res.append(i)
res.append(i+[s[0]])
return res
So far I've sorted out so much, but once you've figured it out, you'll see that all the recursion core ideas are basically the same